Performance des modèles : Attentes et réalité

Quel est votre premier réflexe lorsque votre modèle TAR obtient des résultats médiocres sur un ensemble de contrôle ?

L'idée communément admise est que plus de données d'entraînement (c'est-à-dire plus d'efforts de révision) permettraient d'atteindre les performances souhaitées en termes de rappel et de précision - et avec suffisamment d'argent et de temps, d'approcher les 100 %.

Malheureusement, il faut parfois des centaines d'heures de révision gaspillées avant de se rendre compte que les performances du modèle plafonnent à un niveau loin d'être idéal.

Pouvons-nous anticiper le plafond des performances du modèle, ce qui pourrait nous faire gagner du temps et de l'argent, et nous éviter de décevoir nos attentes ?

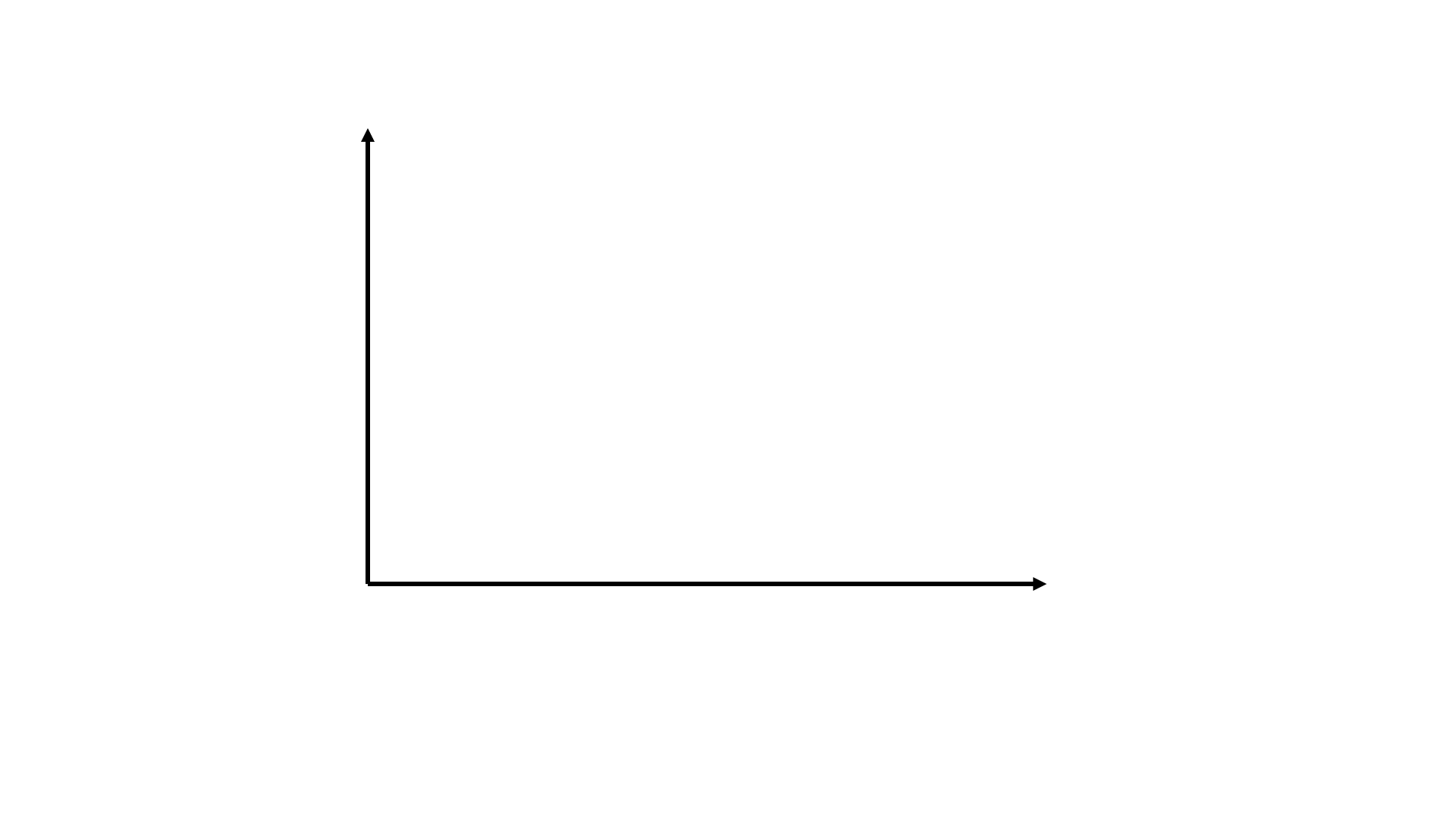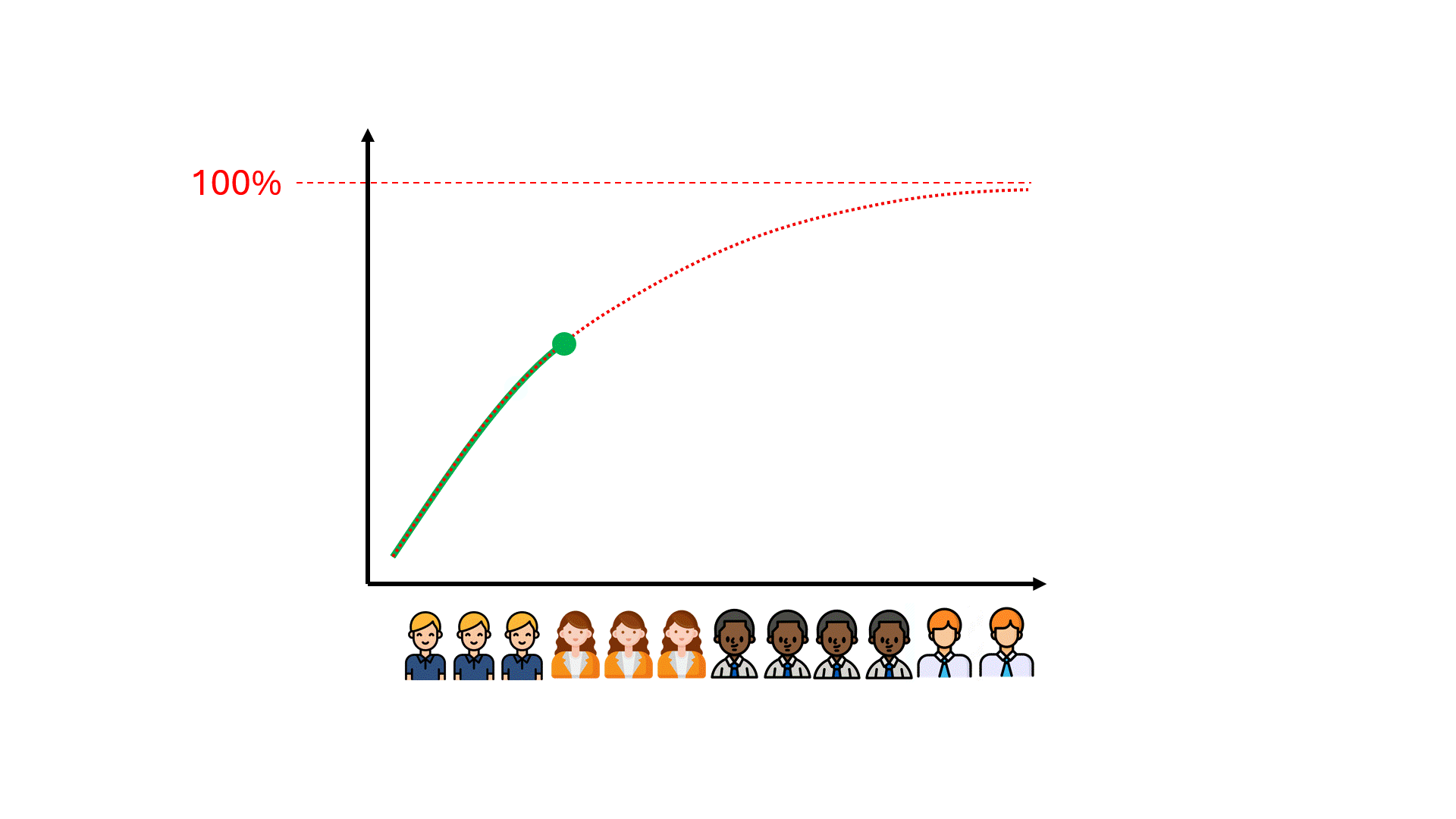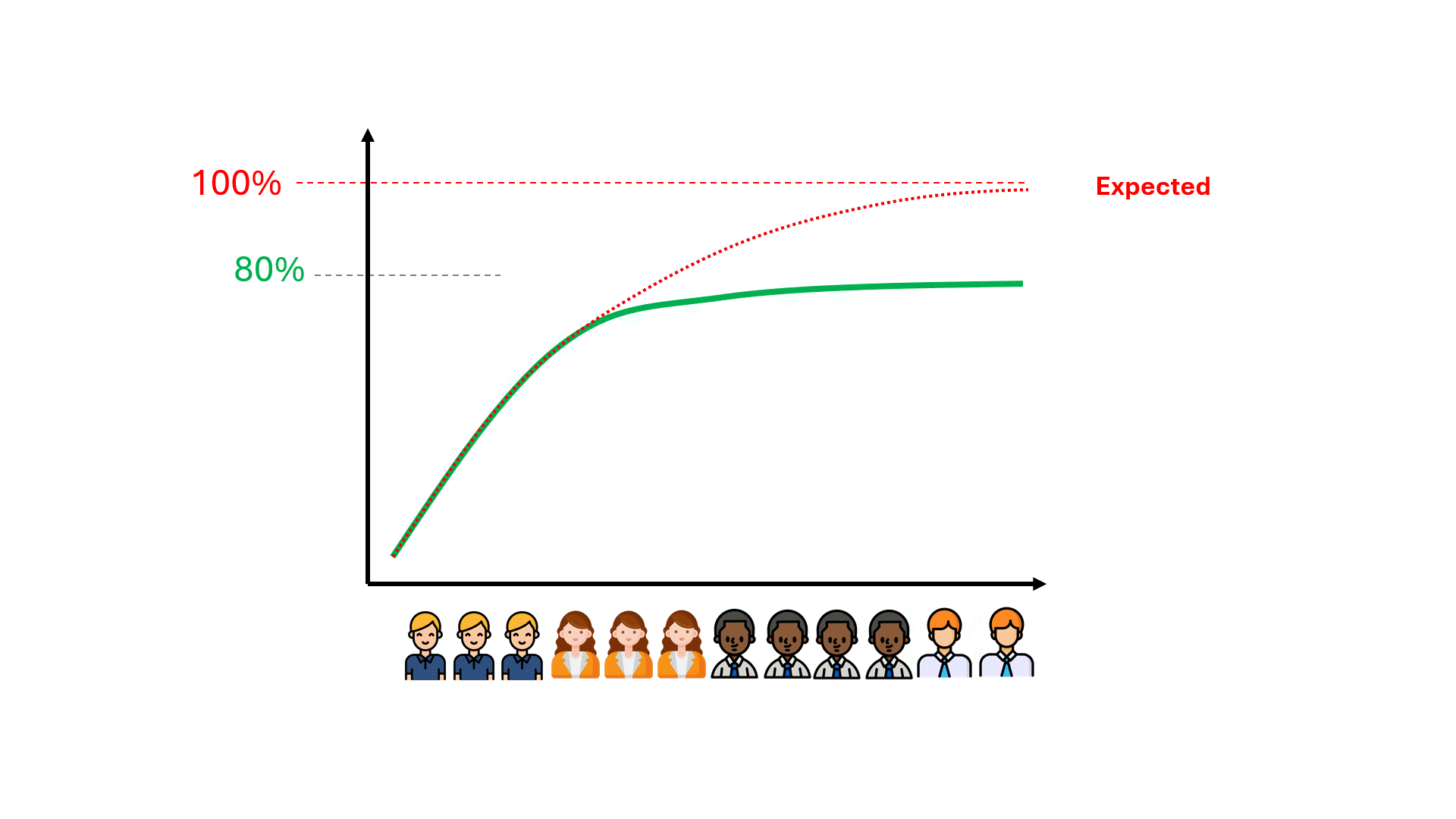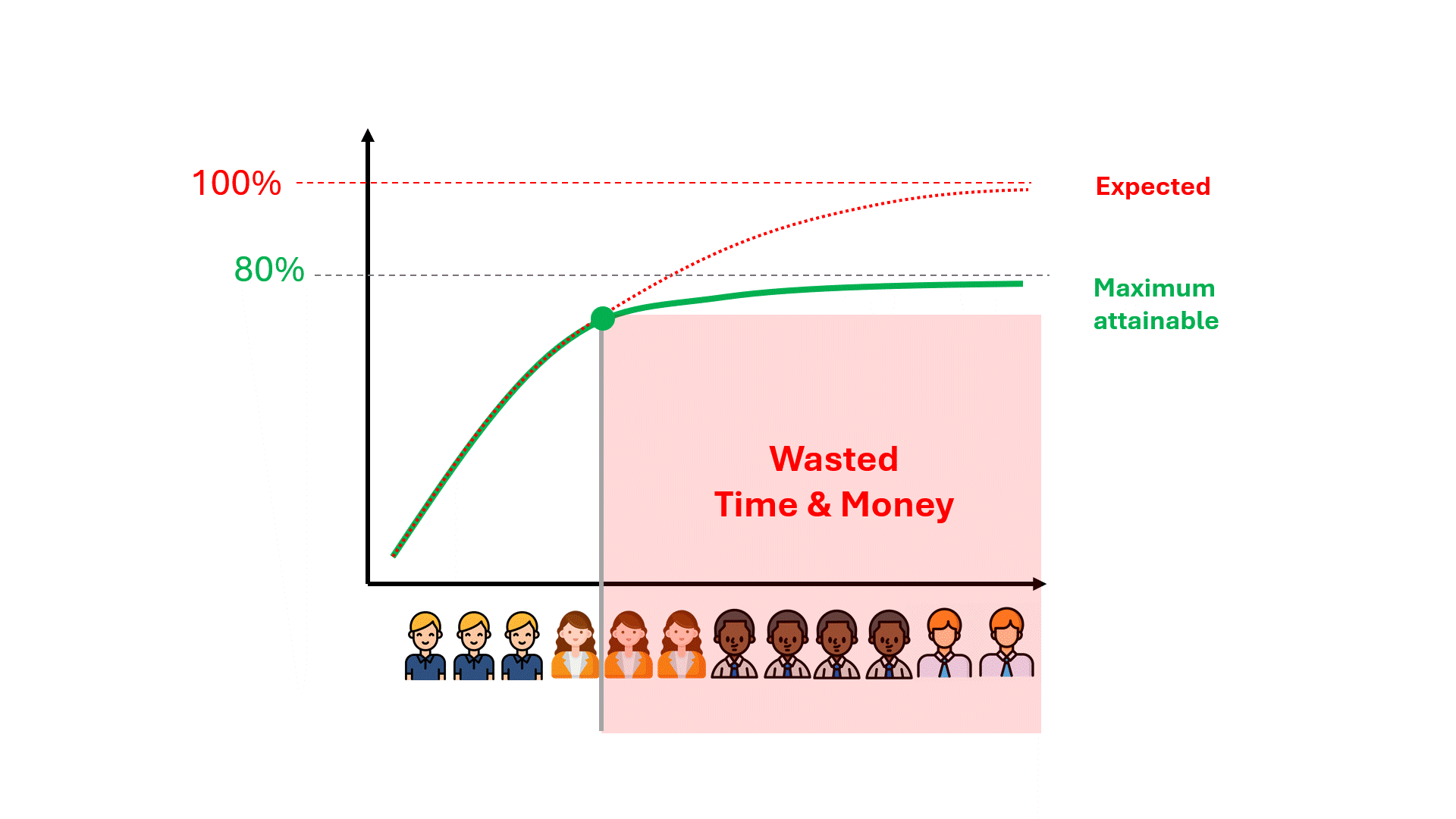
Le plafond de performance est déjà encodé dans vos données

Les données codent certains éléments concernant les performances futures d'un modèle. L'un de ces éléments est le plafond de performance pour des mesures telles que la précision et le rappel. Qu'il s'agisse de TAR traditionnel ou de GPT8, vous pouvez pré-calculer les limites de précision et de rappel, quel que soit le modèle utilisé, en utilisant les données dont vous disposez déjà.

Lorsque nous disons que les données encodent déjà la limite fondamentale des performances de votre modèle, de quelles données parlons-nous - des données d'entraînement ou de test (c.-à-d. l'ensemble de contrôle) ?

En réalité, il s'agit des deux, mais dans cet article, nous nous concentrerons sur l'ensemble de contrôle pour deux raisons essentielles :

1. L'ensemble de contrôle est totalement indépendant du modèle.

2. Il est possible - par de simples calculs mathématiques - de calculer les plafonds de performance.

3. 3. En d'autres termes, en analysant les statistiques de votre ensemble de contrôle, nous pouvons déduire la meilleure performance pour n'importe quel modèle, y compris ceux qui n'existent pas aujourd'hui.

Qu'est-ce qui, dans les données, conduit à des plafonds de performance ?

Bien que les données originales puissent poser problème (par exemple, un texte mal extrait), nous parlons dans cet article d'étiquettes d'examen créées par des examinateurs humains. Il s'avère que les problèmes liés aux données qui conduisent à des plafonds de performance se résument à la nature de l'examen humain.

Il suffit de connaître une seule caractéristique de chaque évaluateur pour prédire le plafond de performance de n'importe quel modèle. Cette caractéristique est le degré de libéralisme ou de conservatisme des évaluateurs dans l'application des étiquettes d'évaluation. D'un point de vue quantitatif, cela se reflète dans leur taux de réponse ou dans la richesse des données qu'ils génèrent.

Pour illustrer pourquoi il s'agit d'un déterminant essentiel du plafond de performance, nous utiliserons deux examinateurs prototypiques - un examinateur libéral qui distribue généreusement l'étiquette réactive lors de la classification des documents, et un examinateur conservateur qui est particulièrement sélectif dans l'étiquetage des documents. En réalité, les évaluateurs se situent sur un spectre en termes d'étiquetage, mais l'illustration des deux extrêmes permettra d'expliquer pourquoi ce phénomène conduit à un plafond de performance.

Expérience de pensée n° 1

Pour comprendre la racine du problème, prenons un exemple très simple.

Imaginons que les évaluateurs conservateurs et libéraux aient entraîné leurs modèles respectifs uniquement sur leurs étiquettes.

Supposons ensuite que chaque modèle soit évalué sur des ensembles de contrôle composés uniquement des étiquettes de l'évaluateur respectif.

Voici une visualisation simple de ce processus. À titre d'illustration, l'évaluateur conservateur a un taux de réactivité de 10 % et l'évaluateur libéral un taux de réactivité de 20 %.

La question est de savoir quelle est la meilleure performance possible, c'est-à-dire le plafond de performance de chaque modèle pour chaque évaluateur.

Si nous éliminons les erreurs ou l'auto-inconsistance de chaque évaluateur, la meilleure performance possible sur chaque ensemble de contrôle serait, bien entendu, de 100 % (100 % de rappel et 100 % de précision) :

Expérience de pensée n° 2

Imaginons maintenant une situation légèrement modifiée : l'ensemble de contrôle du modèle formé par l'évaluateur conservateur a été créé par l'évaluateur libéral, et vice-versa. En d'autres termes, un évaluateur autre que celui qui a formé le modèle a créé l'ensemble de contrôle.

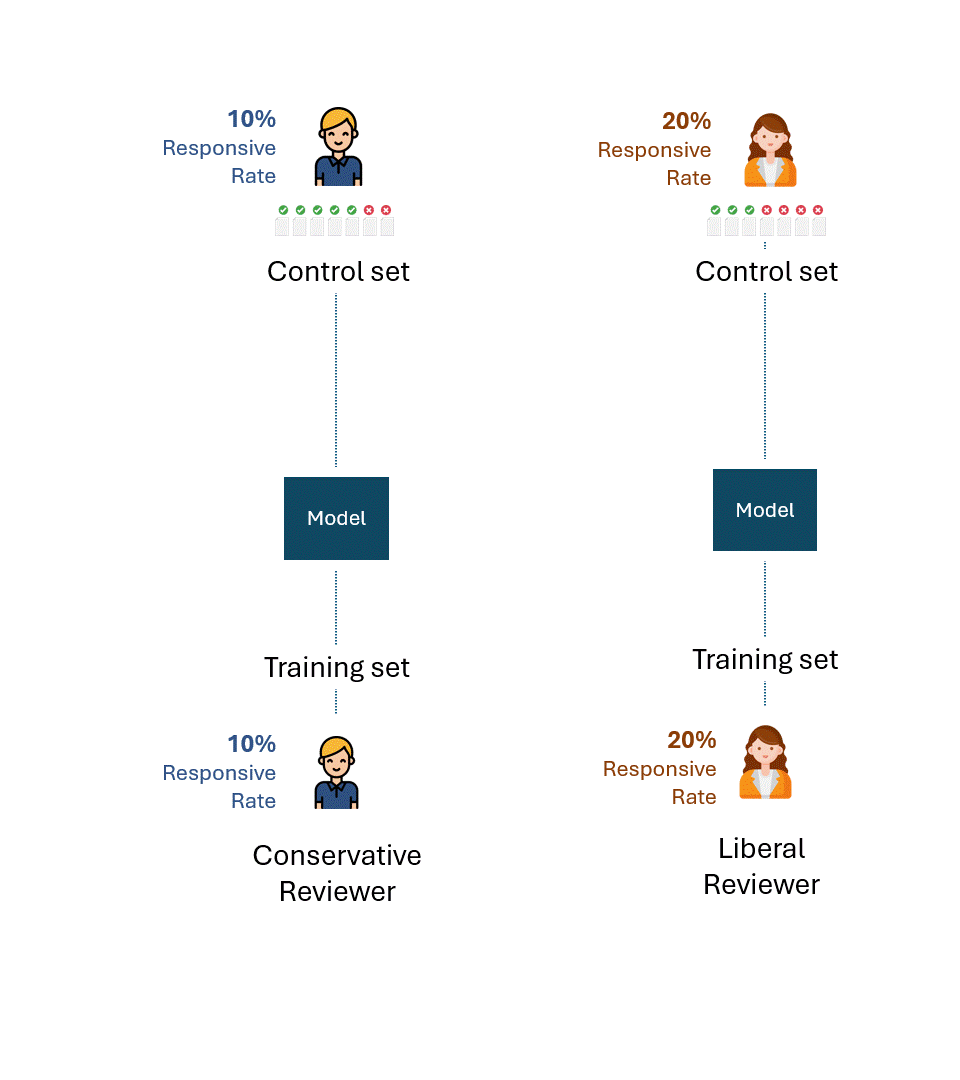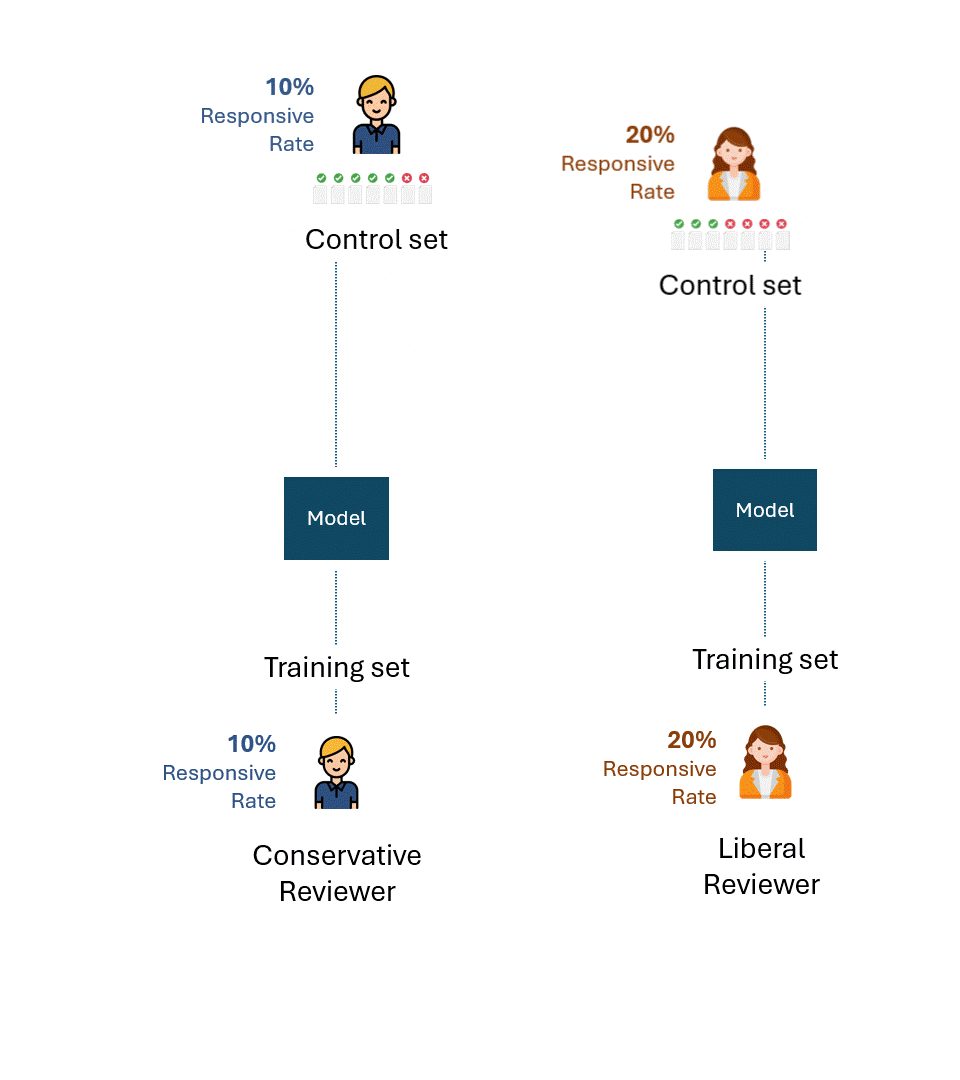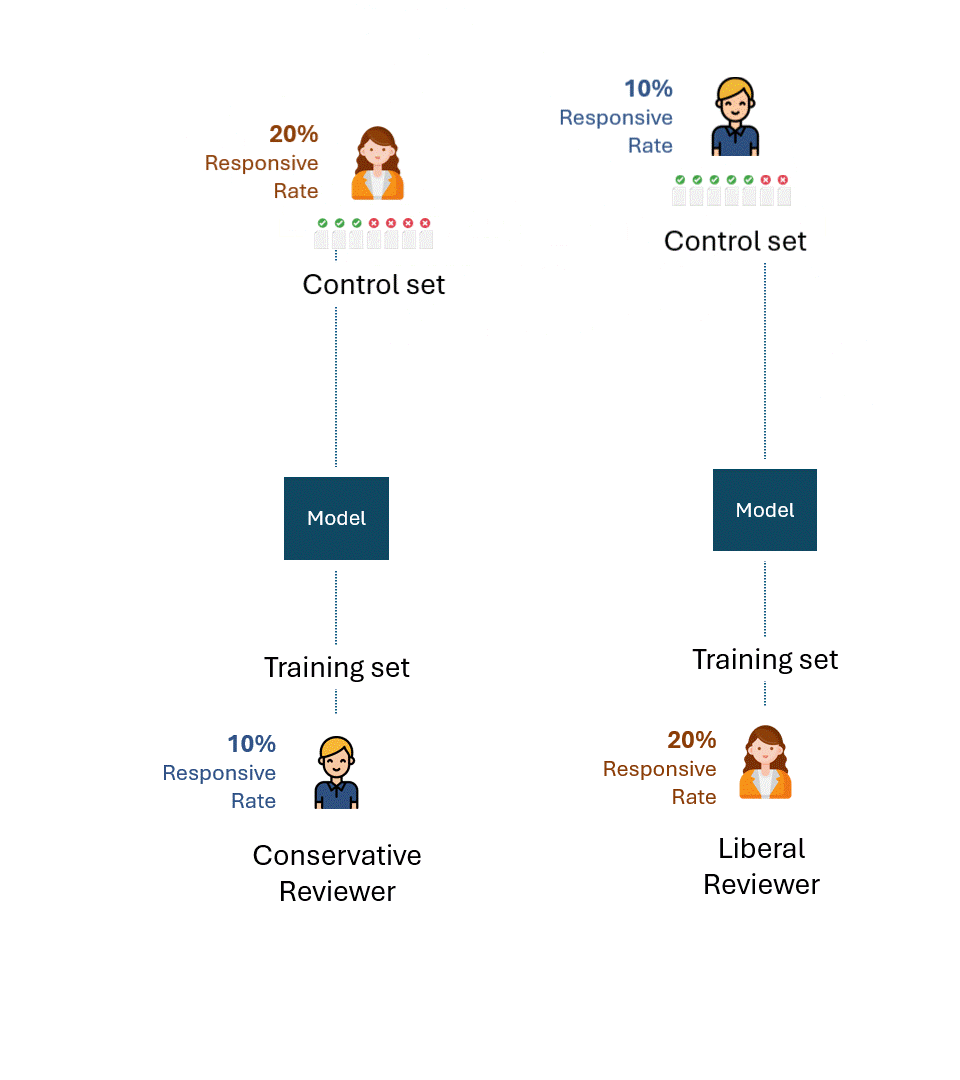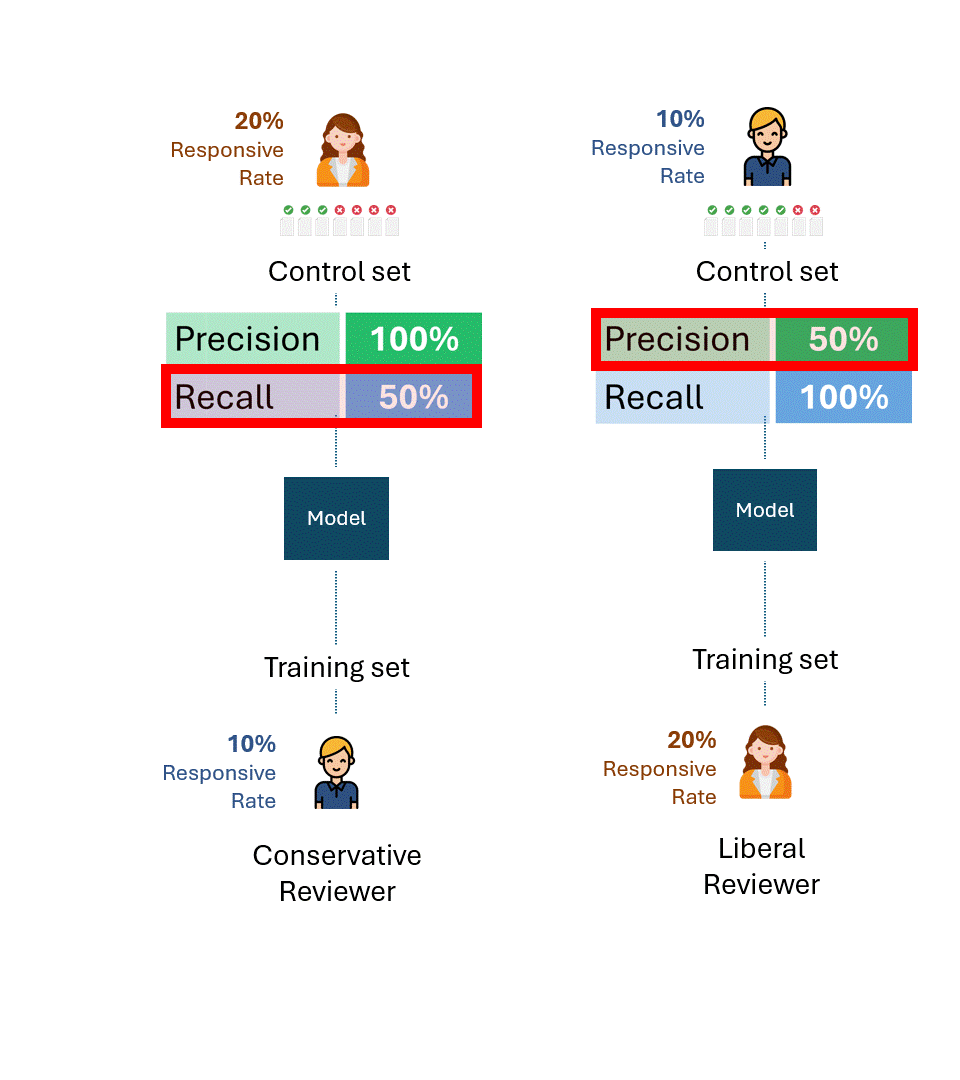
Quelle est maintenant la meilleure performance théorique pour chaque ensemble de contrôle ?

Même si un examinateur libéral créant l'ensemble de contrôle avec un taux de réactivité de 20 % et un examinateur conservateur avec un taux de réactivité de 10 % étaient parfaitement cohérents, ils ne marqueraient que la moitié d'entre eux comme réactifs, soit un taux de rappel de 50 %.

Réfléchissez un instant aux implications de ce constat. L'examinateur conservateur ne peut en aucun cas augmenter ce taux de rappel par le biais d'une formation. Si l'examinateur qui forme le modèle et celui qui le teste (c'est-à-dire via l'ensemble de contrôle) présentaient une disparité fondamentale dans leur taux de réponse, la performance ne pourrait pas s'améliorer au-delà de 50 %.

Qu'est-ce que cela signifie en pratique ?

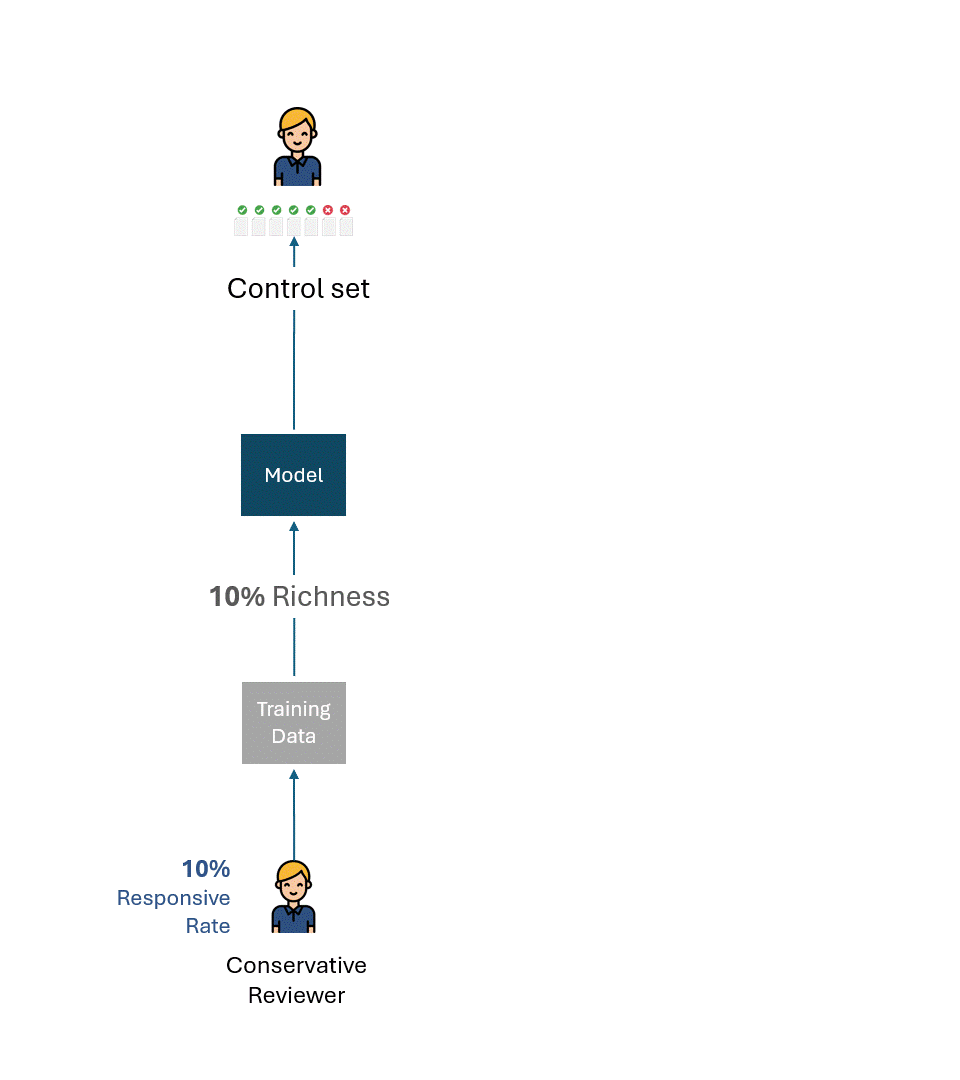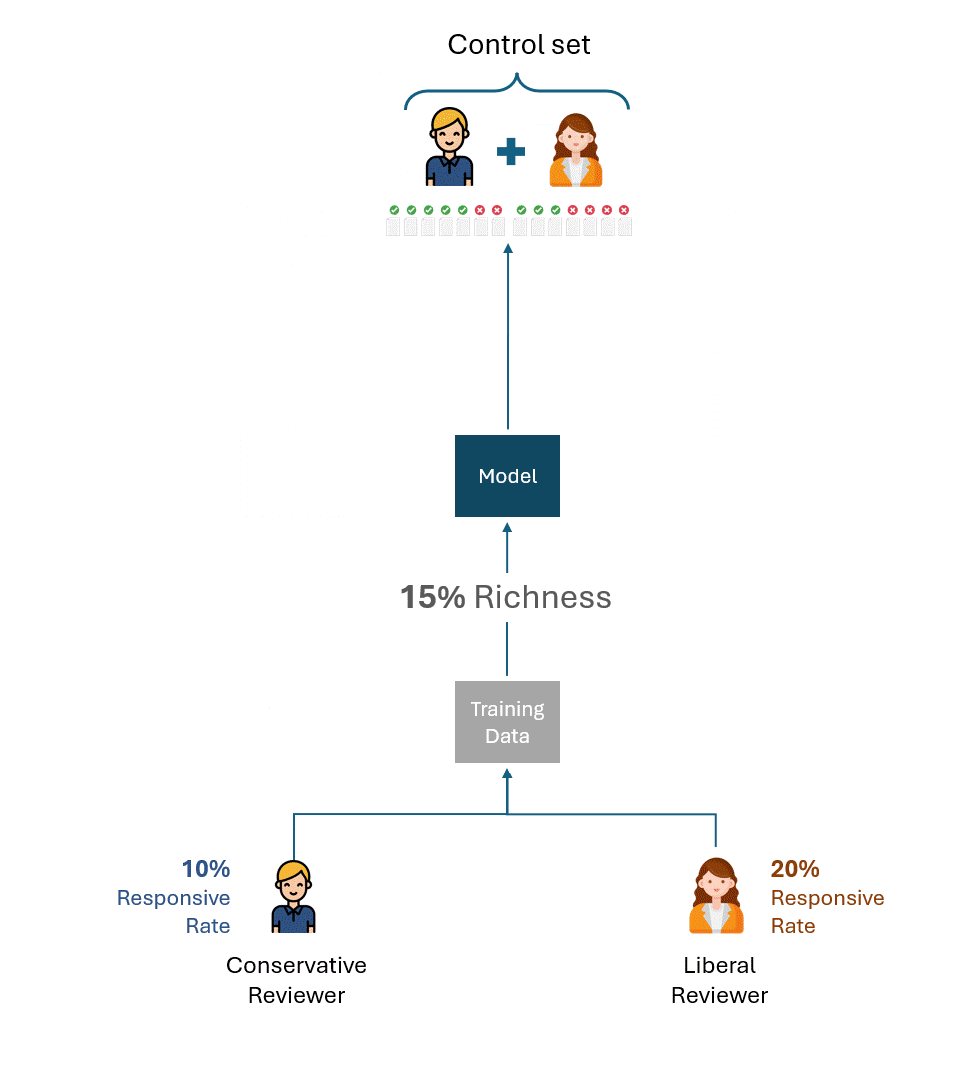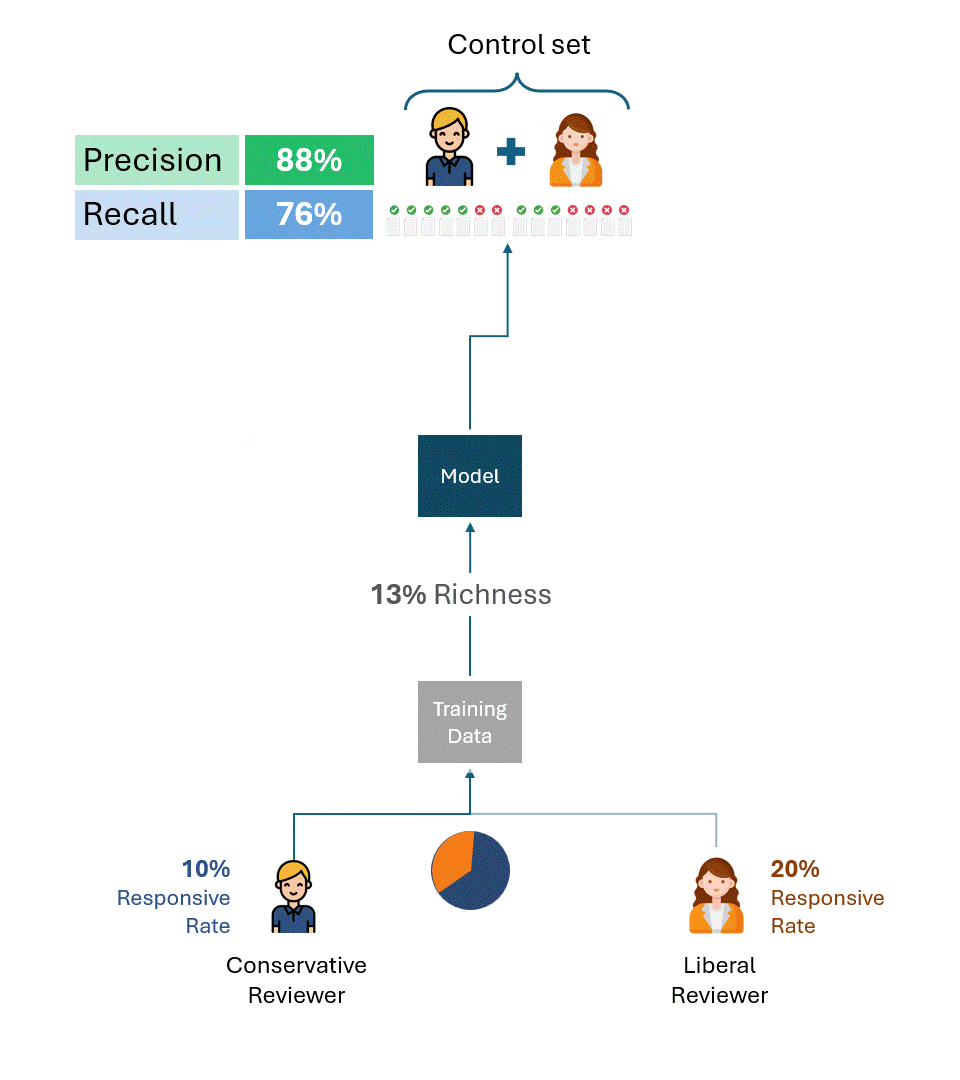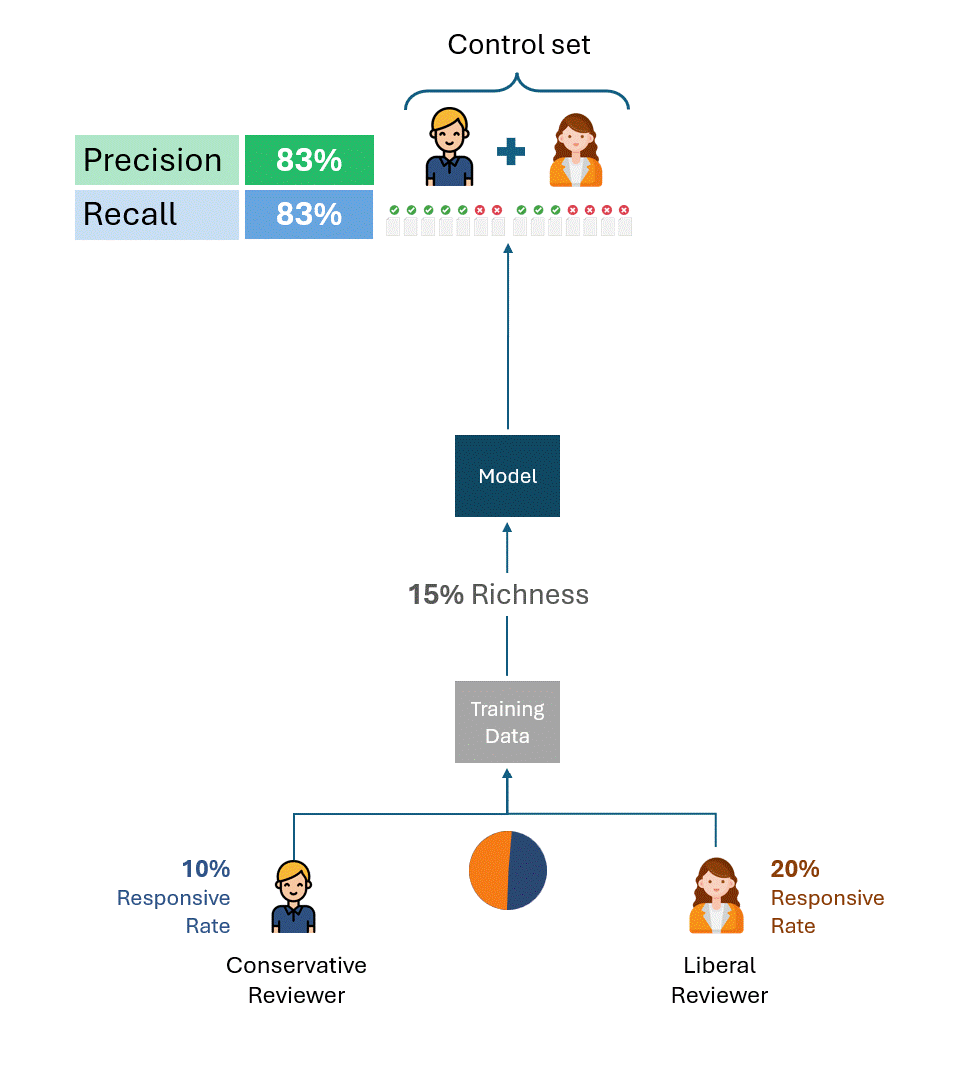
Les exemples ci-dessus sont utiles pour illustrer la cause profonde du problème. Dans la pratique, cependant, plusieurs évaluateurs créent à la fois les données de formation et les ensembles de contrôle, les évaluateurs étant souvent représentés dans des proportions variables, y compris entre les données de formation et les ensembles de contrôle. Bien que cela complique la formule de calcul du plafond de performance, cela ne change pas le résultat fondamental:

Tant que l'ensemble de contrôle contient des étiquettes d'évaluateurs ayant des taux de réponse différents, il existera un plafond de performance totalement indépendant du modèle.

Cela reste vrai quelle que soit la manière dont les données d'apprentissage ont été créées, que ce soit par un seul des évaluateurs (libéral ou conservateur) ou par une combinaison proportionnelle des deux. Le plafond de performance est déterminé uniquement par la disparité du taux de réponse des évaluateurs dans l'ensemble de contrôle.

L'exemple ci-dessous illustre les plafonds de performance des modèles formés à l'aide de proportions variables de données de formation provenant d'évaluateurs conservateurs et libéraux. Comme vous pouvez le constater, aucun scénario ne permet d'atteindre une performance de 100 %.

Igor Labutov, vice-président, Epiq AI Labs
 
Igor Labutov est vice-président d'Epiq et codirige Epiq AI Labs. Igor est un informaticien qui s'intéresse particulièrement au développement d'algorithmes d'apprentissage automatique qui apprennent à partir d'une supervision humaine naturelle, telle que le langage naturel. Il a plus de 10 ans d'expérience dans le domaine de l'intelligence artificielle et de l'apprentissage automatique. M. Labutov a obtenu son doctorat à Cornell et a été chercheur post-doctoral à Carnegie Mellon, où il a mené des recherches pionnières à l'intersection de l'intelligence artificielle centrée sur l'homme et de l'apprentissage automatique. Avant de rejoindre Epiq, M. Labutov a cofondé LAER AI, où il a appliqué ses recherches au développement d'une technologie transformatrice pour l'industrie juridique.